Examples of Singular Value Decompositon

Data compression

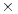Singular value decompositions can be used to represent data efficiently. Suppose, for instance, that we wish to transmit the following image, which consists of an array of 15  25 black or white pixels.

Since there are only three types of columns in this image, as shown below, it should be possible to represent the data in a more compact form.

  

We will represent the image as a 15  25 matrix in which each entry is either a 0, representing a black pixel, or 1, representing white. As such, there are 375 entries in the matrix.

If we perform a singular value decomposition on M, we find there are only three non-zero singular values.

σ₁ = 14.72
σ₂ = 5.22
σ₃ = 3.31

Therefore, the matrix may be represented as

M=u₁σ₁ v₁^T + u₂σ₂ v₂^T + u₃σ₃ v₃^T

This means that we have three vectors v_i, each of which has 15 entries, three vectors u_i, each of which has 25 entries, and three singular values σ_i. This implies that we may represent the matrix using only 123 numbers rather than the 375 that appear in the matrix. In this way, the singular value decomposition discovers the redundancy in the matrix and provides a format for eliminating it.

Why are there only three non-zero singular values? Remember that the number of non-zero singular values equals the rank of the matrix. In this case, we see that there are three linearly independent columns in the matrix, which means that the rank will be three.

Noise reduction

The previous example showed how we can exploit a situation where many singular values are zero. Typically speaking, the large singular values point to where the interesting information is. For example, imagine we have used a scanner to enter this image into our computer. However, our scanner introduces some imperfections (usually called "noise") in the image.

We may proceed in the same way: represent the data using a 15  25 matrix and perform a singular value decomposition. We find the following singular values:

σ₁ = 14.15
σ₂ = 4.67
σ₃ = 3.00
σ₄ = 0.21
σ₅ = 0.19
...
σ₁₅ = 0.05 

Clearly, the first three singular values are the most important so we will assume that the others are due to the noise in the image and make the approximation

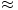M  u₁σ₁ v₁^T + u₂σ₂ v₂^T + u₃σ₃ v₃^T

This leads to the following improved image.

Noisy image	Improved image

Data analysis

Noise also arises anytime we collect data: no matter how good the instruments are, measurements will always have some error in them. If we remember the theme that large singular values point to important features in a matrix, it seems natural to use a singular value decomposition to study data once it is collected.

As an example, suppose that we collect some data as shown below:

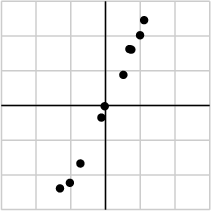
We may take the data and put it into a matrix:

-1.03	0.74	-0.02	0.51	-1.31	0.99	0.69	-0.12	-0.72	1.11
-2.23	1.61	-0.02	0.88	-2.39	2.02	1.62	-0.35	-1.67	2.46

and perform a singular value decomposition. We find the singular values

σ₁ = 6.04
σ₂ = 0.22 

With one singular value so much larger than the other, it may be safe to assume that the small value of σ₂is due to noise in the data and that this singular value would ideally be zero. In that case, the matrix would have rank one meaning that all the data lies on the line defined by u_i.

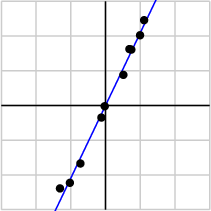
This brief example points to the beginnings of a field known as principal component analysis, a set of techniques that uses singular values to detect dependencies and redundancies in data.

In a similar way, singular value decompositions can be used to detect groupings in data, which explains why singular value decompositions are being used in attempts to improve Netflix's movie recommendation system. Ratings of movies you have watched allow a program to sort you into a group of others whose ratings are similar to yours. Recommendations may be made by choosing movies that others in your group have rated highly.

References:

• Gilbert Strang, Linear Algebra and Its Applications. Brooks Cole.
  
  
• William H. Press et al, Numercial Recipes in C: The Art of Scientific Computing. Cambridge University Press.