Hybrid Hierarchical Clustering
Lately in
class we have been studying a technique to draw inferences on data called
Clustering in which we try to understand various data points’ relationships to
one another by assigning them into groups or clusters, usually based on
Euclidean distances apart from one another. It’s underlying purpose is to try
to help represent data points which are similar and cluster those points while separating
clusters from other clusters that are not similar. In class, we discussed
two methods for clustering. They were Agglomerative and Division.
Agglomerative means bottom up clustering wherein one would
start with an individual point and then gradually accumulate the next nearest
point to form a cluster over and over until there are no points close enough to
qualify to be included in the cluster. It Kind of makes me imagine a small
alien blob swallowing up other small close by alien blobs until it becomes a
much bigger alien blob. This method is particularly
good at finding smaller clusters. Typically, bottom up clustering works well
when a large number of clusters are required.
The division method is essentially opposite of Agglomerative
in approach. It starts with A very large set of points, and gradually divides
them by recursively splitting them. This method is good for finding large clusters.
The division method works well when a small number of clusters is required.
Alright, now on to what this blog post
is really about. I felt like that review was necessary because the actually
subject of this blog pertains to a hybrid clustering method based on these two
distinct techniques being combined, in a way. Its purpose is to combine the
strengths of both methods. This hybrid clustering method is based on the
concept of “The mutual cluster.”
Essentially, a mutual cluster is a group of
points that are close enough to each other and far apart from one another that
they shouldn’t be separated. Mutual clusters are still essential formed based
on the distance of one point to another point. The criteria to form a mutual cluster is given like this. "The largest distance between any
two points within the mutual cluster must be smaller than the distance between
any points within the mutual cluster to a point that is not in the mutual
cluster. In that sense, an entire data set is actually a mutual cluster."
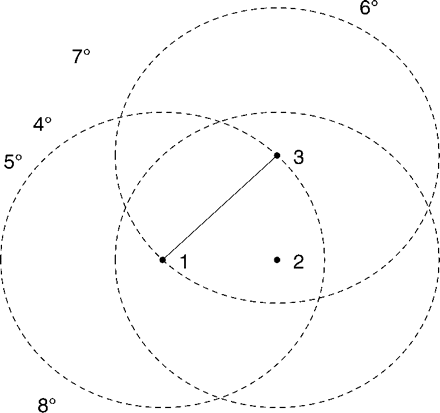
If you look at the illustration of a mutual cluster from the article below, you will
see that we have the points 1,2, and 3. The greatest distance between these
points is the distance between one and three. The circles in this illustration show that distance 360 degrees around each point. If
no points fall within these circles, than {1,2,3} would be a mutual cluster.
Say however, a new point 9 fell very
close to 1, then {1,2,3} would cease to be considered a mutual cluster.
However, it is possible that the new point 9 could fall into a position such
that the cluster would become {1,2,3,9}.
That is the understanding I have drawn
on mutual clusters from the article. Now I will go into detail as to how a
mutual cluster assists in a “hybrid” method.
>>>>>>>>>>>>>>>>>>>>> outcomes of the three different techniques. The polygons are being used to
indicate the “nested clusters” which is just essentially a cluster within a
cluster. Note that all three methods have clustered in different ways. How do
you know which one is “most right?” I’m actually asking that as a question. Perhaps
someone could elaborate on that with a comment on this post. I would think it
would depend on what kind of question a person might be asking about the data,
or maybe what the data actually represents or its format or the number of
clusters intended to be created.
To finish off this post, I will describe, as
best as I can understand from the article, the procedure of the hybrid method
and the strengths and weaknesses of this method. The procedure for this method
is as follows:
The first step is that the mutual
clusters are to be computed by the criterion I described earlier in the post.
The second step is to the “constrained” top down method. It uses the word “constrained”
because it is not allowed to break up the mutual clusters. Top down methods
tend to like to split things up, like divorce lawyers. The third step of this
method must be performed after the top down procedure in step two has been
completed. The third step involves performing a top down clustering inside each
of the little mutual clusters.
My idea I have gotten about this after 2
hours of lulling over the incredibly complicated looking math lingo in the
article is this. Mutual clusters are like giving ‘protective shells’ to certain
groups of data points early on so that the top down method cannot break them
up. That is my ‘laymen terms’ explanation of this to myself. Perhaps someone
else has a better way of thinking of it?
The article goes over verious simulation
experiments to evaluate the effectiveness of the method over a variety of
different data situations and validate its usefulness. I am going to skip over that and
allow anyone who is interested to read that.
The paper concludes by discussing the
strengths and weaknesses of using the method. One strength is that the mutual
clusters are very intuitive when deciding what points should be included. But
the weakness in the hybrid method is that sometimes the proximity circles
around the data points of mutual clusters is just a hair short enough to not
include other data points that are actually still pretty close to the cluster.
That at least, is what I gather in my mind from the article. I found it
interesting.
References:
The authors of the Article I did my post
on are Hugh Chipman and Robert Tibshirani. This paper can be found at this
link.

Wade,
ReplyDeleteThank you for making this post and sharing this reference. I believe this is very useful to many people.
Fadel